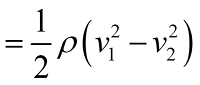daniel Bernoulli
นักวิทยาศาสตร์ชาวสวิสส์
(ค.ศ.1700-1782)
พลศาสตร์ของของไหลเป็นการศึกษาของไหลที่มีการเคลื่อนที่ โดยสมมติให้ของไหลเป็นของไหลอุดมคติ พฤติกรรมของของไหลอุดมคติอธิบายได้ด้วย สมการความต่อเนื่อง (the equation of continuity) สมการของแบร์นูลลี (Bernoulli's equation) และ หลักของแบร์นูลลี (Bernoulli's principle) ความรู้เกี่ยวกับหลักการของแบร์นูลลีนำไปใช้อธิบายการทำงานของอุปกรณ์บางอย่าง เช่น เครื่องพ่นสี การทำงานของปีกเครื่องบิน เป็นต้น รวมทั้งใช้อธิบายปรากฏการณ์บางอย่างในชีวิตประจำวัน
จะได้สูตรสมการแบร์นูลลี
P1 คือ ความดันบรรยากาศ
v1 คือ ความเร็วของระดับผิวน้ำ ซึ่งมีค่าระดับลดลงช้ามากๆ จนเข้าใกล้ 0 เราจึงกำหนดให้เป็น 0 ซะเลย (เนื่องจากถังน้ำมีขนาดใหญ่มากๆ)
ด้วยซ้ายของสมการ คงเหลือเพียง Pressure Head และ Elevation Head
พิจารณาด้วยขวาของสมการ ซึ่งได้ข้อสรุปว่า
P2 คือ ความดันบรรยากาศ (ความสูง h2 มีค่าน้อยมากไม่ทำให้ความดันแตกต่างจากที่ผิวของไหล)
h2 มีค่าเป็น 0 เนื่องจากเรากำหนดระดับอ้างอิง ตรงตำแหน่งรูรั่วพอดี
ด้านขวามือของสมการคงเหลือเพียง Pressure Head และ Velocity Head สมการแบร์นูลลีจึงเหลือเพียง
จะได้
สรุปว่า ความเร็วของน้ำที่ไหลออกจากรูรั่ว มีค่าเท่ากับวัตถุที่ตกอย่างอิสระจากความสูง h1
รูปแสดงภาพตัดส่วนปีกของเครื่องบิน และสายกระแส ของอากาศ จุดที่ 1 และ 2 ปีกของเครื่องบินได้รับการออกแบบให้เป็นดังรูปเนื่องจากต้องการให้อากาศที่ไหลผ่านด้านบนของปีก(จุดที่ 1) ต้องมีความเร็วมากกว่าด้านล่างของปีก (จุดที่ 2) หากความเร็วมีความแตกต่างกันแล้ว จะทำให้เกิดอะไรขึ้น ใช้สมการของ แบร์นูลลี เข้ามาช่วยวิเคราะห์ได้ดังนี้
สิ่งที่ทำให้การวิเคราะห์ง่ายขึ้นคือ ความหนาของปีก มีค่าน้อยมากๆ เมื่อเทียบกับระดับเพดานบิน ทำให้เราสมมุติได้ว่า h1 = h2 จึงได้ว่า
หรือเขียนสมการได้ว่า
เนื่องจาก v1 มากกว่า v2 เนื่องจากการออกแบบปีกเครื่องบิน มีผลทำให้ด้ายขวาของสมการเป็นบวก ส่งผลให้ด้านซ้ายของสมการต้องมีค่าเป็นบวกด้วยนั้นคือ P2 มีค่ามากกว่า P1(แรงดันที่ด้านล่างของปีกมีค่ามากกว่าแรงดันจากด้านบนของปีก)
จากความดันที่แตกต่างกันจึงทำให้เครื่องบินสามารถยกตัวเองให้ลอยขึ้นในอากาศได้
หากเราทำให้ความเร็วลมบนปีกเครื่องบินแตกต่างจากความเร็วลมใต้ปีกเครื่องบินมากขึ้นเท่าใด
ปีกเครื่องบินด้านบนก็จะมีความดันแตกต่างจากปีกด้านล่างมากขึ้นเท่านั้น ส่งผลให้เครื่องบินลอยได้ และ บรรทุกสัมภาระได้น้ำหนักที่มากขึ้น
หากเราทำให้ความเร็วลมบนปีกเครื่องบินแตกต่างจากความเร็วลมใต้ปีกเครื่องบินมากขึ้นเท่าใด
ปีกเครื่องบินด้านบนก็จะมีความดันแตกต่างจากปีกด้านล่างมากขึ้นเท่านั้น ส่งผลให้เครื่องบินลอยได้ และ บรรทุกสัมภาระได้น้ำหนักที่มากขึ้น